Transformations

http://blog.naver.com/slime321/50013775951

만약에 당신의 computer graphics modeling system 이 모든 object 들에게 같은 위치와 같은방위,  같은 크기 만을 제공하여 줄 수 있다면... 그 modeling system 의 사용은 극히 제한적으로 이루어 질 수 밖에 없을 것입니다..

　

우리가 실제로 작업을 하기 위해서는 공간상에서 object 를 움직이고..

그것의 방위를 회전 시키며.. 크기를 바꾸어 줄 수 있어야 합니다..

이러한 세 가지의 변화를 합쳐서 우리는 transformations 라고 부르게 됩니다..

　

우리가 작업 공간에서 object 의 위치를 바꾸어 주는 것을 그 object 를 Move 혹은 Translate시킨다.. 라고 부르게 됩니다..

object 를 이동시키게 될 때 우리는 three - dimensional coordinate system 에서 사용하였던개념을 그대로  적용 시키게 되어 집니다..

우리가 앞에서 다루었던 three axis 의 coordinate system 에서의 위치 개념과 동일하게 생각 하시면 됩니다..

　

일반적으로 object 를 움직이게 되면 object 는 three axis   즉 X, Y, Z 방향으로 이동하게

되고 ..  이렇게 이동 되어진 값을 우리는 translation X, translation Y, translation Z 로 이야기하게 되고.. translate x,y,z 혹은 translate (x,y,z) 또는 move x,y,z 로 부르게 되어 집니다..

　

예를 들어 translate ( 5, 3, -2) 로 표현되어 진다면...

X 방향으로 5 만큼 이동하고, Y 방향으로 3만큼 이동하고, Z 방향으로는 음의 방향으로

2만큼 이동하였다는 의미를 갖게 됩니다..

 

 

 

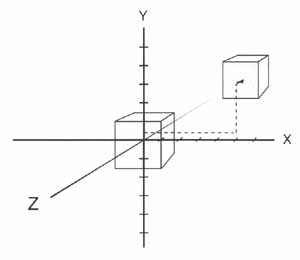
                                               Fig 1

 

그림 1 의 cube 는 원점 (0,0,0) 에서 오른쪽으로 5만큼 , 위쪽으로 3만큼 뒤쪽으로 2만큼

이동하였다는 것을 알 수 있습니다.. 위의 (5,3,-2) 란 위와 같은 형태의 움직임을 이야기

하게 되는 것입니다..

　

object 이 움직임에서 기울기나 방향의 전환이 발행하도록 움직이는 것을 우리는 rotate

라고 부르게 됩니다..  이것은 가장 기본적인 transformation 의 두번째 형태 입니다..

　

rotate 에 대한 이해를 위해 아래의 그림 처럼 밀랍 인형이 서 있는 형태를 생각해 보도록

하겠습니다..

 

 

 

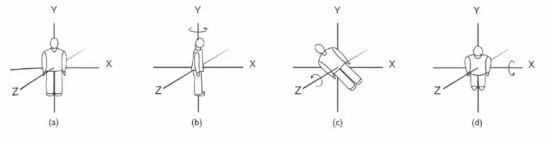
위의 그림 (a) 의 경우를 보면 머리가 위를 향하고 발이 아래로 향한 채 꼬챙이에 꽃혀 꽂꽂이 서있는형태를 보여 주고 있습니다..

그림 (b) 의 경우 처럼 Y axis 에 의해 회전하는 형태를 보여 준다면 우리는 "Y 축으로 회전 한다" 라고 이야기 하게 됩니다..

그림 (c) 는 Z 축으로 회전하는 모습을 보여 주고 있고 , (d) 의 경우는 X 축으로 회전하는 모습을 보여주고 있습니다..

이러한 회전은 한 점을 출발하여 다시 그 지점으로 되돌아오는 것을 완전한 회전으로 생각하여 360도의 값으로 나타내어 집니다..

어떤 시스템에서는 degree 보다는 radians 를 단위로 사용하기도 하는데 One radian 은 57.29578 degree의 값을 가지게 됩니다..

　

Rotations  와 같은 translations 는 일반적으로 3 가지의 값을 가지고 사용되어 지게 되는데 이 세 가지의값은 각각 X rotation, Y rotation, Z rotation 입니다.. Rotate (90,0,0) 라고 한다면 이것은 X 축으로 90 도를회전 하였고 Y 나 Z 축으로는 변화가 없다는 것을 의미하게 됩니다..

　

이러한 표현에서 한가지 생각해 보아야 할 것은 우리가 X 축으로 90 도 회전 하였다 라고 이야기 할때 X축에서 어떤 방향으로 회전하였다는 말이 되는 걸까요?

이것에 대한 정의를 내리기 위하여 먼저 엄지 손가락을 세운 뒤 네 손가락을 쫙 펼쳐 줍니다..

 

 

 

 

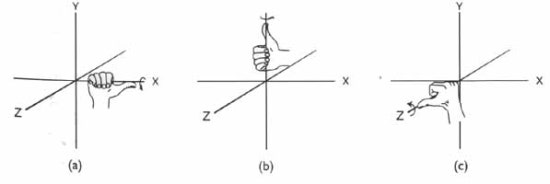
위의 그림에 나타난 것과 같이 손가락들이 축에 위치한 상태에서 엄지 손가락이 축의 방향을가르키도록 위치 시켜 줍니다..

오른 손을 이용한 이러한 작업을 우리는 right -handed rotation 이라고 부르게 됩니다..

그림처럼 엄지 손가락을 원하는 축의 방향을 향하도록 한 후 움켜진 방향으로 의 회전이 right-handed rotation 에서 증가하는 양수의 값을 가지는 회전으로 정해지게 됩니다..

이때 이러한 방향의 설정은 앞장에서 다룬 적이 있는 coordinate system 과 연관성을 가지게 됩니다..

　

coordinate system 에서 left - handed coordinate system 과 right - handed coordinate system 을 생각해 보게 되면..

　

만약 left-handed coordinate system 에서 위의 그림 a 와 같이 X 방향을 오른쪽으로 지정하여 주게 되면 Z 축을 제외한 X와 Y 축의 방향은 right - handed coordinate system 과 동일하게 되지만 Z 축의 방향은 역전되게 되어 집니다..

바꾸어 이야기 하자면 left-handed coordinate system 과 right-handed coordinate system 에서의 위와 같은 handed rotation 방식의 가장 큰 차이점은 회전하는 방향이 서로 역전되어 진다는 것입니다..

　

이러한 이유로 인한여 표준적인 방법이 제시되지 않는다면 rotation 에서의 방향 문제는 많은 혼란을 가져 올 수도 있게 되므로 rotation 이 right-handed direction 이냐? 아니면 left-handed direction 을 따르고 있느냐? , software 가 right-handed coordinate system 을 사용하느냐?  아니면 left-handed  coordinate system 을 사용하느냐는 아주 중요한 문제입니다..

　

위의 그림에 적용되어진 것은 right - handed coordinate system 과 right - handed rotations 을 사용한 것인데.. 대부분의 animation package 들이 이러한 조합을 사용하고 있다고 이해하고 있어도 큰 무리가 없을 것 입니다..

　

transformation 의 세번째 형태로는 object 의 size 에 변화를 주게 되는 Scale 이 있습니다..object 의 Scale 역시 세 개의 축에 의지하여 변화하게 되는데...

만약에 object 가 한 축을 따라 scale 에 변화를 주게 되면 size 는 한 방향으로만 변화 가 됩니다..

 

 

 

 

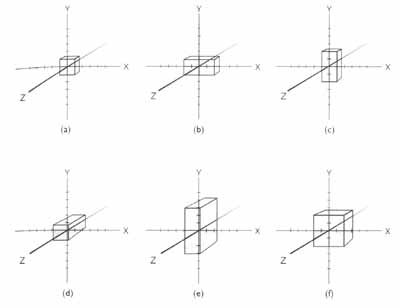
위의 그림 에서 a 는 기본 상태의 cube 를 나타내고 있습니다..

b 의 경우는 X 축을 따라 scale 을 변화 시킨 경우를 나타내고 있고...

c 의 경우는 Y 축을 따라 ... d 는 Z 축을 따라 변화 한 것을 나타내고 있습니다..

매우 일반적인 이야기 이긴 하지만 scale 은 하나나 혹은 그 이상의 axis 를 따라 변화하게 됩니다..

e 의 경우는 y 와 z 축을 따라 크기의 변화가 생긴 경우를 나타내고 있습니다..

　

object 가 scale 의 변화를 주면서 처음 상태의 비율을 계속하여 유지하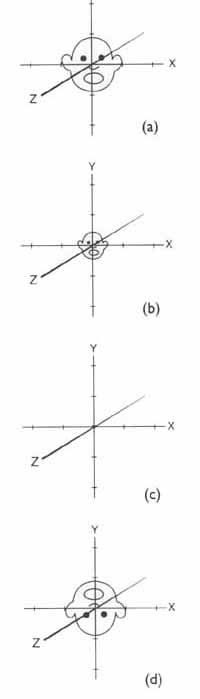지 않는 것을 우리는 ..nonproportional scale. 또는 nonuniform scale 이라고 부르게 됩니다..

　

반대로 처음 상태의 비율을 계속하여 유지한다면 우리는 그것을 proportional scale 혹은 uniform scale라고 부릅니다..

scale transformation 역시 다른 transformation 과 동일하게 3 개의 숫자를 사용하여 표시 되어 집니다.

 

3 개의 숫자는 각각의 축을 나타내게 되는데..

위의 그림에서 f 를 예로 들게 되면 uniformly 상태인 이 object 는 세 개의 축의 값이 모두 같습니다..

예를 들자면 (2,2,2) 라는 식으로 말입니다...

nonproportional scale 을 예로 들어 X 축으로 2, Y 축으로 3, Z 축으로 7 이라고 생각해 보면.. 이것은 (2,3,7) 이라고 표시되어 질 수 있습니다..

 

동일한 크기로 변하는 scale 의 변화에 대하여 는 위와 같은 표시 이외

 

에 한 자리의 숫자로 표시 하는

것이 가능한데.. 만약 0.5 라는 값이 주어지게 된다면.. 크기가 절반으로 줄어 들게 됩니다..

만약 cube 의 vertex 가 각각 (6,6,6) 에 위치하고 있는 cube 를 0.5 라는 값으로 변화를 주게 되면..

vertex 의 위치는 (3,3,3) 으로 변화하게 되는 것입니다..

그리고 scale 에 (-) 의 값을 부여하게 되면 .. flip 이나 invert 효과를 가져오게 됩니다..

예를 들어 (2,5,8) 이라는 scale 값을 가지고 있는데 (2,-5,8) 이라는 식으로 scale 에 변화를 주게 되면..

Y 방향이 바뀌게 되어 Y 방향으로 반전되는 효과를 가져오게 된다는 의미 입니다..

( 그림 2 참조 )

 

  Fig 2

                                                                           

자 .. 이제 기본적인 세 가지의 transformations 에 대하여 알아보았습니다..

여기에서 한가지 경우를 생각해 보도록 하겠습니다..

당신이 0,0,0 지점에 서 있는데 move 3,0,0 란 이야기를 듣고 3,0,0 지점으로 이동하였다고 생각해 봅시다

다시 당신에게 move 3,0,0 란 명령이 주어지게 된다면 당신은 그것을 어떻게 해석 하시겠습니까?

3,0,0 지점으로 이동하라고 한다고 생각 한다면 이미 그곳에 위치하고 있으니 움직일 필요가 없겠지만

3,0,0 만큼 더 이동하라고 이해 한다면 다시 움직여 주어야 할 것입니다..

　

이러한 비슷한 예로 일상생활에서 위치를 가르쳐 주는 경우를 생각해 본다면..

어느거리 몇번지 어느 집이라고 분명하게 가르쳐 줄 수 있는 경우가 있는데 ..

이러한 것을 우리는 absolute transformation 이라고 이야기 하게 됩니다..

three - dimensional coordinate system 에서 absolute locate 는 직접 위치를 명시하여 주는 것을 말

하는데 " move absolutery (3,0,0) " 라고 한다면 우리는 (3,0,0) 지점으로 이동하여 주면 됩니다..

　

또 다른 형태로는 현재 위치한 지점에서 상대적으로 움직일 거리를 지정하여 주는 방법이 있습니다..

이러한 방식을 우리는 relative transformation 이라고 부르게 됩니다..

이러한 예를 들어 보자면 " 거기서 2블록 위로 올라와서 코너를 돌아 4번째 건물.." 정도가 되겠지요..

"move relatively (3,0,0)" 라고 한다면 현재의 위치에서 (3,0,0) 의 값을 더하여 주면 된다는 의미 입니다..

 

                                         

 

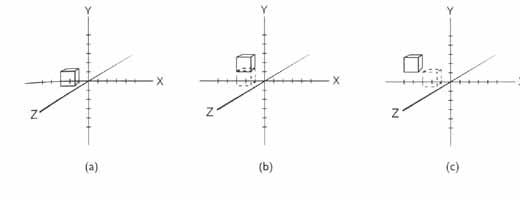
이러한 차이는 위의 그림을 보면 분명히 알 수 있습니다..

(a) 의 위치가 (-2,0,0) 라고 한다면 absolute move (-2,1,0) 라는 명령이 주어지게 되면 이미 -2 의 위치에

있는 cube 는 X 방향으로는 움직이지 않고 Y 방향으로만 움직이게 될 것입니다..(b)

만약 relative move (-2,1,0) 라고 주어지게 된다면 현재의 위치에 (-2,1,0) 의 값을 더해 주게 되므로

(-4,1,0) 의 지점으로 이동하게 될 것입니다..(c)

 

위에서는 단순히 translation 에 대하여만 예를 든 것이지만 다른 두 가지의 transformations 에 대하여도

동일하게 적용되어 집니다..

rotate 에 대하여 예를 들어 보게 되면..

그림 3 의 a 와 같은 형태에서 X 축으로 45 도 rotate 하라는 명령을 주게 될때에..

현재 a 에서 90 도의 각을 가지고 있는 board 가 absolutely 상태에서는 b 와 같이 움직이게 되고 ...

relatively 상태에서는 90 도에 45 도가 더해져서 그림 c 와 같은 형태로 움직이게 될 것입니다..

 

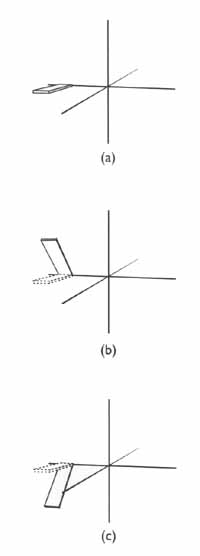
                                                              fig 3

 

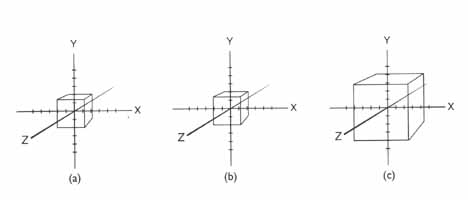
scale 을 예로 들게 되면...

위의 그림에 나타난 것과 같이 이미 2 라는 scale 값을 가지고 있는 a 의 cube 에 다시 2 라는 scale 값

이 주어지게 된다면...

absolute acale 상태에서는 전혀 변화가 일어나지 않게 되지만... (b)

relative scale 상태에서는 object 의 sale 이 다시 2배로 증가하게 됩니다...(c)

 3D gomputer graphics system 작업에서 absolute 와 relative 의 적용 상태에 대하여는 미리 알고 있는 것이 좋으며.. 대부분의 software 들은 이러한 구분이 가능한 기능들을 제공하여 주고 있습니다..

실제로 우리가 작업할때에도 상대좌표와 절대좌표라는 표현으로 이러한 기능을 적절히 사용하고있습니다..

 

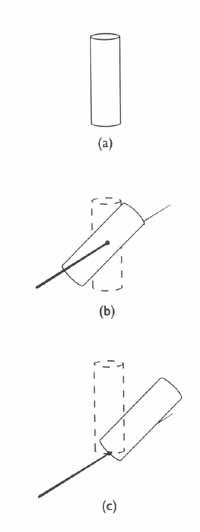
자.. 이제 그림 4와 같은 cylinder 가 있다고 가정하여 봅시다..

우리는 이 cylinder 를 회전 시키기 위해서 중심점을 (b) 처럼 cylinder 의 center 에 위치 시켜 줄 수도

있고 그림 (c) 처럼 cylinder 의 아래에 위치 시켜 줄 수도 있게 됩니다..

　

이 point 를 우리는 pivot point , 혹은 local origin 이라고 부르게 됩니다..

여기에서 우리는 transformations 와 관련해서 이해해야 될 것이 있는데 .. 그것은 world coordinate

system , 혹은 global coordinate system 이라고 불리우는 것과 local coordinate system 이라는

것입니다..

local coordinate system 이 개별적인 object 의 pivot point 를 중심으로 작업이 이루어 진다면..

world coordinate system 은 작업공간의 한 지점을 전체 object 의 작업 중심으로 작업이 이루어 지게

됩니다.                                              fig 4

 

 

 

 

 

 

 

 

local coordinate system 에서 local origin 이 어느 에 위치하고 있느냐에 따라 아래 그림과 같이 전혀 다른 움직임이 보여 질 수 있게 됩니다..

 

 

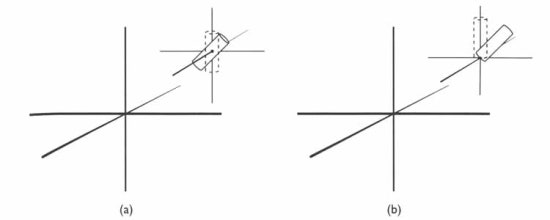
또한 world coordinate system 과 달리 local coordinate system 에서는 object 의 움직임에 따라 object 의 origin 도 함께 움직이게 됩니다..

아래 그림의 a,b 는 동일하게 (5,3,0) 라는 지점에 위치하고 있습니다..

하지만 서로의 local origin 의 위치가 다르므로 서로 동일하게 위차하고 있지 않은 모습을 보여 주게 되는 것입니다..

 

 

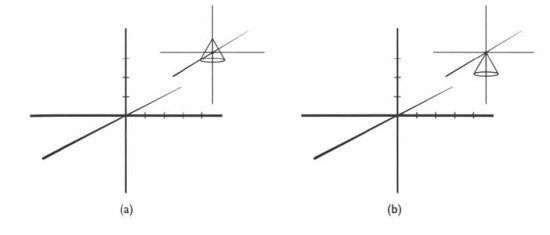
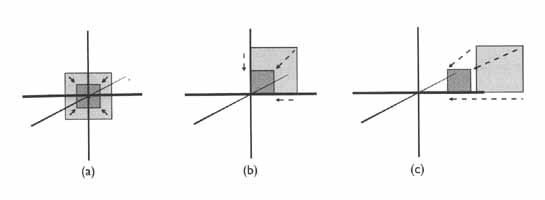
scale 을 예로 들게 되면 아래 그림은 cube 에서 각각의 local origin 의 위치에 따른 scale 의 변화에서의 모습을 보여 주고 있습니다..

 

 

만들때 마다 다르기는 하지만 일반적으로 object 를 만들기 위한 변형의 순서가 있게 됩니다..예를 들어 램프의 갓을 만들고자 한다면 .. 먼저 적당한 크기로 cone 을 조정하여 줄 것이고..그것을 lamp 의 상단 부위에 위치시키게 될 것입니다..

그리고 적당한 위치를 조절하여 주고.. 다시 움직여 주고.. 회전 시켜 주고.. 크기를 조금 수정하여 주고.. 위치를 조금 수정하여 주고..

　

이러한 모든 변형은 3D modeling system 안에서 세 개의 기본적인 transformation 을 하나의 set 으로 압축한 형태로 나타내어 지게 되는데..

이렇게 여러 가지의 transformation 을 하나의 transformation set 으로 엮어주는 것을 ..

concatenation of transformations 라고 합니다..

그 결과는 9개의 transformation 값으로 연결 되어진 형태로 나타나게 되는데..

3개의 translation 값과.. 3개의 rotation 값과.. 3개의 scale 값으로 나타나게 되어 집니다..

이렇게 9개의 값을 그림 5와 같은 형태로 배열하여 준것을 "matrix" 라고 부르게 됩니다..

( 복수의 matrix 를 matrices 라고도 합니다..)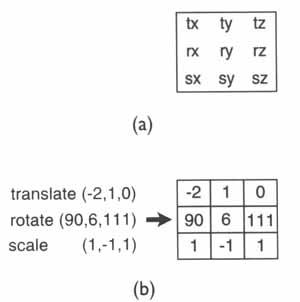

그리고 이러한 것을 transformation matrix 라고 합니다..        

이렇게 변형을 일종의 도식화 하여 배치하여 주는 것은 수학적인 관점에서 볼때 개발자들이 손쉽게 변형값을 사용하여 조작할 수 있도록 할 수 있도록 하기 위하여 중요한 의미를 갖게 됩니다..

그림 5의 a 는 일반적인transformation matrix 의 배치를 나타내어 주고 있고.. 그림 5의 b 는 transformation 값이 배치 되어진 모습을 나타내어 주고 있습니다..                      fig 5

 

 

우리가 object 를 만들고 아무 변형을 가하지 않았다 하더라도.. 그것은 이미 변형을 가지기 전의 transformation값이 적용되어진 상태입니다..

이렇게 move, rotate, scale 의 변화가 주어지지 않은 transformatio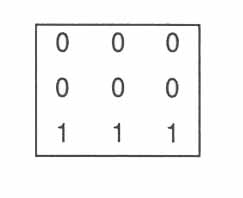n 의 값을 default 상태라고 하는데.. 이러한 default transformation 이란 다른 말로 이야기 하자면..move (0,0,0); rotate (0,0,0); scale (1,1,1) 로 표시되어 질 수 있습니다..그리고 이렇게 변형을 주지 않은 값을 우리는 identity transformation 이라고 부르기도 합니다.. ( 그림 6 )

이 identity transformation 값은 우리가 작업 중 object 의 transformation 값을 없애기를 원할 때 되돌아가는 기본이되는 값이 기도 합니다.                                            fig 6

 

 

transformation matrix 라는 이러한 개념은 3D computer graphics 의 중심적인 개념입니다..

그리고 이러한 개념의 연장선에서의 기술의 예를 들어 보게 되면..

이러한 기술이 포함될 수 있는 경우로 한 scene 에 여러개의 같은 object 가 존재 한다고 생각해 보면..

 

 

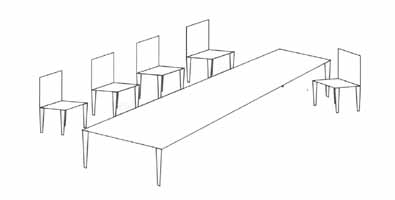
위의 그림에서 알 수 있듯이 이 경우는 위치와 방위만이 다를 뿐인 많은 의자가 존재 하고 있게 됩니다..

우리는 computer graphics developed 에서 이러한 종류의 modeling 상태에 대한 기술을 instantiation 이라고부릅니다....

이러한 instance 는 copy 와는 다른 개념입니다..

copy 의 경우는 geometry 를 복제하여 주는 것 입니다..

instance 의 경우에는 model 의 geometry 를 duplicate 하지 않습니다..  다만...

software system 은 " 그 위치" 라는 개념만을 가지고 있습니다..

그렇기 때문에 copy 와는 달리 원 모델에 대한변화가 모든 object 에 동일하게 적용되어 지게 되는 것입니다..

여기에서는 새로운 geometry 의 형태를 만들어 주지는 못합니다..

그러므로 여러분이 original model 에서 instance 상태로 model 을 만들어 주게 된다면...

그것은 하나의 geometry 와 두 개의 transformation matrices 로 정의 되어 질 것입니다..

 

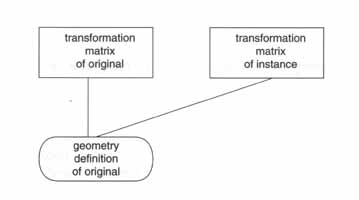
이러한 방식은 data 의 관리라는 측면에서도 매우 경제적이지만..

한번의 작업으로 동일한 모든 model 에 변형을 줄 수 있기 때문에 많은 object 가 포함되어 지는 scene 에서는 매우 유용하게 사용되어 질 수 있습니다..

[출처] Transformations|작성자 slime321